The Origin of Gravity

>> Mass-free Gravity <<

The acceleration of a particle in free fall is caused by the refraction of its oscillating components by a cloud of exchange particles.
This also explains the weakness of gravity and the fact that its effect is
only an attractive one.

- It also includes all the phenomena of General Relativity. -


0   Abstract

According to present understanding of physics, gravity is described by Einstein's general theory of relativity. Here gravity is a geometric phenomenon described by a four-dimensional system of space and time. It is curved in the general case and is formally described by Riemannian geometry.

An alternative way of viewing gravity is to use the fact that the speed of light is reduced in a gravitational field. Time is represented by the internal oscillations of elementary particles. Einstein originally tried to develop general relativity along these lines. His 1911 paper "Über den Einfluss der Schwerkraft auf die Ausbreitung des Lichts" ["On the influence of gravitation on the propagation of light"] was a first step into this direction. Unfortunately, Einstein's paper contains a false assumption and its consequences seem to have discouraged Einstein from pursuing this path.

This calculation not only gives the gravitational behaviour of an object at rest, but also explains the acceleration of fast-moving objects in a gravitational field, which is usually explained using Einstein’s general theory of relativity ("curvature of space-time"). The refraction of light-like objects by the field is an equivalent but simpler alternative to Einstein’s model of space-time curvature.

Here we will show that this approach works extremely well.

1   Introduction

 It is a well known fact that the speed of light is reduced in a gravitational field. As a result, a light beam passing a massive object will be deflected towards that object. This deflection can be quantitatively explained by the refraction of the light due to the gravitational potential. - The same thing happens to any light-like particle.

From the spin and the magnetic moment of an elementary particle it can be concluded that the constituents of such particles are in constant oscillation travelling at the speed of light c. In the case of the electron, this was determined by Paul Dirac in 1928. Applying the effect of refraction to this oscillation within an elementary particle, it yields the correct gravitational acceleration of a free physical object in a gravitational field.

This calculation not only gives the gravitational behaviour of an object at rest, but also explains the acceleration of fast-moving objects in a gravitational field, which is usually explained by Einstein’s general theory of relativity ("curvature of space-time"). The refraction of light-like objects by the field is an equivalent but simpler alternative to Einstein’s model of the curvature of space-time.

And, very surprisingly, we find that the mass of an object is not the cause of its gravitational field.

This understanding of gravity eliminates the problems of dark matter, as photons fulfil the functions of dark matter in all occurrences.

And it explains the problem of dark energy and the very serious problem of quantum gravity.

The structure of particles used here is called the Basic Particle Model.

(Note: This site is also available as a pdf file)
  

2   Bending of a Beam of Light Passing a Massive Object

The speed of light is not constant in the vicinity of matter but depends, in the case of the sun for example, on the gravitational potential as follows:

 

(2.1)

where c is the speed of light in gravity-free space, credu is the reduced speed of light in the field, G is the gravitational constant; M is the mass of the source, which is traditionally said to cause the gravitational potential; and r is the distance from the centre of the gravitational source. The power p is 1/2 or 1 depending on the direction of motion with respect to the centre of gravity; it is 1 for the radial direction and 1/2 for the tangential one.

This equation was determined experimentally for the first time by the Shapiro experiment in 1970 for small changes in c.

(Remark: Equation (2.1) can also be derived using Einstein’s general theory of relativity. We will not use Einstein’s theory here, but instead quote the experimental result as such. Later we will derive the equation from physical considerations in contrast to the structural considerations used by Einstein.)

From classical optics, it follows that a light beam passing through a region in which the speed of light depends on its position is deflected towards the region in which the speed of light is lower.

 


Figure 2.1: A light-like object deflected by a massive object
 
 

The deflection of a light beam passing the sun was correctly stated for the first time by Albert Einstein. He predicted the gravitational acceleration of the photon to be twice the value of the Newtonian acceleration (as first predicted by von Soldner in 1801). This has historically been taken as important proof of Einstein’s concept of a 4-dimensional curved space-time. We will, however, see that Einstein’s concept is not necessary to achieve this result. A calculation based on the classical assumptions of refraction yields the same result.

2.1 The Size of the Deflection

There now follows a brief collection of equations, which describe the deflection of the path. A detailed deduction of the refraction process is given in Appendix A (pdf-version).

The first step necessary is to take the derivative of c with respect to the direction y - perpendicular to the path of the particle (y being equal to d at the vertex). And we define x as the distance between the point being considered and the vertex of the path.

We can now describe the radial distance r in terms of the components x and y:

   

(2.2)
 

Taking into account the dependency of the reduction of c on x and y, which follows in a somewhat complex way from equations (2.1) and (2.2), we get
   

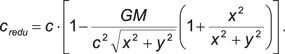(2.3)
  Taking the derivative of this equation with respect to y yields
   


(2.4)
  Here we assume that the deflection is small (i.e. α < < 1, so (x,y) describes an almost straight line).

We can then determine the differential angle of deflection, dα, by applying the classical mechanism of refraction and assuming credu ≈ c. : 		 
   


(2.5)
  If we now replace r and x by ϑ, the angle between the direction of the vertex of the path (i.e. the closest position to the sun) and the actual position, and y by d in eq. (2.4) we get
   

(2.6)
  Integrating equation (2.6) over ϑ from ϑ = -π/2 to ϑ = π/2 yields  
   

(2.7)
  Inserting the appropriate values
 

-  G = 6.674 · 10-11  m3 kg-1 s-2
-  M = 1.989 ·1030 kg
-  c0 = 2.998 · 108 m s-1
-  d = 6.95 · 108 m

 
  and converting to degrees, we get the correct result of
 

1.75 arc-sec .

 
  This corresponds to twice the classical gravitational acceleration (Newton) and agrees with observation. Both the numerical result and the analytical result (2.7) also conform to the predictions of general relativity – however without resorting to general relativity and space-time curvature.

2.2  The Acceleration

Next we will need the acceleration of the beam at the vertex of the path. The acceleration a within the beam depends on the angle of deflection α as follows:
     

(2.8)
  Inserting (2.5):
   

 
  into this we get
   

(2.9)
  Now using (2.4):
       
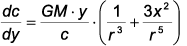  yields
   

(2.10)
  At the vertex, x = 0 and y = r, giving
    (2.11)
  which is the value of the Newtonian acceleration for this particular position.
 



3   Relationship between Gravity and the Basic Particle Model


3.1 The Structure of Elementary Particles

The above chapter was about gravity at high velocity. Next we have to understand the effect of gravity on an object at rest.

To understand further implications of the refraction process for the phenomenon of gravity, we have to investigate the general structure of matter, i.e. the structure of elementary particles.

From the dynamic parameters of an elementary particle, its spin and its magnetic moment, and also from its relativistic behaviour it follows that a particle is made up of two sub-particles, which we will call "basic particles" and which orbit each other at the speed of light c as shown in figure 3.1.
   
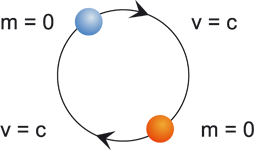Figure 3.1: Basic Particle Model
 
Top 
  This structure was in principle already found by Erwin Schrödinger in 1930, when he analysed the Dirac function of the electron and found that there must be a permanent internal oscillation at the speed of light c. He gave this oscillation the German name "Zitterbewegung" ("ZBW").

The Basic Particle Model assumes that this structure is valid for all leptons and also for all quarks.


3.2 Conditions for the Refraction of an Elementary Particle

In textbooks which deduce gravitational lensing by classical means, the refraction of light or light-like particles in a situation with a varying speed of light is normally explained by means of a pair of photons or a pair of particles. However, we have to assume that a single object is subject to refraction too. So, a basic particle is also subject to refraction in the appropriate situation.

This is a necessary assumption at this point in order for the following considerations to apply. It can be logically understood from the point of view of the particle, if we assume that even a basic particle has an extension (a kind of charge cloud, which may be arbitrarily small) or it is in a state of permanent oscillation.

3.3 Gravity Acting on an Object at Rest

3.3.1 Gravitational Acceleration in a Special Orientation

If an elementary particle is placed in a gravitational field, its basic particles are subject to refraction as explained above. This refraction causes the basic particles to deviate from their circular path. This will in turn cause the entire elementary particle to move.

If we take an elementary particle oriented in such a way that its orbital axis points towards the source of the gravitational field, then refraction causes the basic particles to spiral towards the source of the field. Hence the entire elementary particle will move in the direction of the source. Due to refraction, the pitch angle of the basic particles, α, will steadily increase. This causes the elementary particle to perform accelerated motion towards the gravitational source.
 
   


Figure 3.2: Progressive spiralling downwards
 
Top

 
  Figure 3.2 shows the downward accelerated motion. Note that only the path of one of the two basic particles is shown here to keep the drawing simple.

In this case the acceleration of the (composite) elementary particle is similar to the acceleration given in equation (2.11)
   

(3.1)
  which is again the value of the Newtonian acceleration.

3.3.2 Gravitational Acceleration in Arbitrary Orientations

In the general case, the orientation of the axis is at an arbitrary angle θ with respect to the vertical direction
(see figure 3.3).

   

Figure 3.3: General orientation of a particle
 
Top 
  In this case only the projection of the refraction in the vertical direction is effective for gravity. This means on the one hand that the gravitational acceleration is reduced compared to the case discussed above. However, on the other hand, this reduction is compensated for by an increase in the refraction of the vertical component as seen in eq. (2.10), i.e. the term with a factor of 3.

So in the case of an arbitrary orientation of the elementary particle too, we can get the result given in eq. (3.1)
     
 

which is the well-known result for the classical case (Newton).
 

4   The Equivalence Principle

4.1 Equivalence Classically

The (weak) equivalence principle deals with the fact that every object undergoes the same gravitational acceleration independently of its mass.

In order to explain this fact, Newton introduced the equivalence principle, saying that there exists an inertial mass and a gravitational mass. Both types of mass are said to be equivalent to a high degree, and consequently the gravitational force acting on an object is strictly proportional to the inertial force, so that every object undergoes exactly the same acceleration in a particular gravitational field.

When Einstein developed the general theory of relativity, he adopted this principle and made it to one of the pillars of his theory.

Neither Newton nor Einstein ever attempted to explain this phenomenon in physical terms.
 
4.2 Equivalence Based on the Particle Model

Looking at figure 3.2, it is obvious that the deflection of the path of the basic particles is independent of the radius of the particle and, because of the particle model used here, independent of the mass of the particle. So the fact that the gravitational acceleration is independent of the mass has a very natural cause. No assumptions about any equivalence are needed.

Figure 3.2 shows why an elementary particle at rest is subject to gravitational acceleration. It is in fact gravitational lensing on a microscopic scale.

This is the physical cause of the independence of gravitational acceleration from the mass of an object.
 



5   The Schwarzschild Solution

Working with Einstein’s field equations is an extremely challenging task. A short time after Einstein published his general theory of relativity, Karl Schwarzschild presented a solution for the simpler, less general situation of a spherically symmetric field, like the one surrounding the sun, which is a very common case in astronomy. The experiments and observations cited in the literature as proving Einstein’s general theory of relativity usually refer to the results of the Schwarzschild solution.

According to the Basic Particle Model, an elementary particle is made up of two sub-particles orbiting each other. Their temporal behaviour is given in the following equation describing the proper time of an object in motion, as it is normally a part of special relativity:

    (5.1)
  Here t is the time as measured in the system at rest, and τ in fact describes the development of temporal processes in the system in motion. Taking the derivative of this equation with respect to t and squaring and rearranging the result, we get:  
    (5.2)
 

In a gravitational field this time-dependent behaviour changes. The understanding of this change guides us directly to the Schwarzschild solution.

Since the Schwarzschild solution is normally presented in polar coordinates, we first split the speed into its radial and tangential components:

 
    (5.3)
  where vrad and vtan denote the radial und the tangential components of the speed with respect to the centre of the gravitational source.

Now we have to take into account the fact that c changes in a gravitational field in the following way according to (2.1):
     
Top
  where p is 1/2 or 1 depending on the direction of motion in respect to the centre of gravity.

Furthermore, the size of the elementary particles changes in the gravitational field because the speed of light c changes in the field. By taking this fact into account when using eq.(5.3) we get – as deduced in detail in the appendix B:
    (5.4)
  The equations are usually simplified by defining the so-called Schwarzschild radius rs
    (5.5)
  and we can also denote the derivative with respect to t by a prime. This leads to:
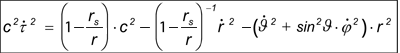    (5.6)
  which is a popular way of writing the Schwarzschild solution.

A detailed deduction is given in appendix B of the pdf-version.


6    The Cause of Gravity

We have seen that gravity is in fact not a force but a refraction process. And the cause of this refraction is the variation in the speed of light c in the vicinity of matter.

6.1 The Variation of the Speed of Light

Equation (2.1) is the basis for explaining all phenomena associated with gravity. Now we have to understand this dependency.

The reduction in c can be explained by the exchange particles, which are associated with the binding field between
the basic particles.

According to the Basic Particle Model, the binding field is the field due to the strong interaction, which is – also according to the model – the universal force in our world which affects all existing particles. These exchange particles, which effect an attraction or a repulsion in a random way, also interact with all light-like particles. They cause such a particle to be deflected towards the origin of the exchange particle (which is the basic particle) or away from it. So the light-like particle performs a random walk as depicted in figure 6.1. As a result the average speed of the light-like particle is reduced, even though its microscopic speed is still the speed of light c.

   


Figure 6.1: Disturbance in the path of a light-like particle
 
Top 
  According to the Basic Particle Model, the field due to any basic particle is made up of a similar collection of elementary charges (of the strong field), and it is therefore independent of the type of elementary particle to which the basic particle belongs. Hence the flow of exchange particles is also independent of the type of particle. Consequently the reduction in c and thus the gravitational effect is also independent of the type of particle, which means that it is independent of the size and consequently independent of the mass of the elementary particle. Every elementary particle provides the same contribution to the gravitational field.

This understanding contradicts conventional physics, but it helps to overcome the principle problems of present-day gravitational physics.   

Remark: The above explanation may appear to conflict with the fact that the forces within an elementary particle in the binding function have a limited range. This seems not to conform to the infinite range of the gravitational field. The solution is that the binding field is set up as a multi-pole field by an arrangement of monopole charges, producing the strong force. The exchange particles of these monopole charges, which cause the disturbance in the path of a light-like particle, have an unlimited range as we know from the case of electric charges.

6.2 Speed Reduction in Detail

As mentioned above, the reduction in c is caused by the continuous deflection of the light-like particle. This magnitude of this reduction will now be determined.

We will consider two orthogonal cases, the motion in the tangential direction with respect to the centre of gravity, and in the radial direction. In the tangential direction the reduction is given by

    (6.1)
 

as this is a perpendicular disturbance of the path. In the radial direction it is
    (6.2)
 

which is greater than in the former case, being a longitudinal disturbance of the path.

The effective size of the effect on the speed depends on two factors

  1. The influence of a single exchange particle
  2. The rate of incidence of exchange particles.
     
As the influence of the exchange particles adds up in a random way, the resulting deflection depends on the square root of the rate of incidence of the particles and therefore on the square root of the number of particles N causing the gravitational field. The rate further depends on the distance between the particles which form the source of the gravitational field and the point under investigation. Combining all these, the resulting equation is
    (6.3)
  where again p =1 for radial motion and p = 1/2 for tangential motion.

Furthermore, the extension of the binding field in an elementary particle and hence the size of any objects in a gravitational field is given by the equation
     
 

Here we have used N to denote the number of elementary particles causing the gravitational field, to reflect the fact that this influence is independent of the mass of a particle. And so we have to use a different gravitational constant, denoted here by g.

The derivation is given in detail in Appendix C of the pdf-version.

 

7  Present Problems with Gravity
  1. Dark Matter: It is at present not understood why a rotating galaxy is a stable configuration. By conventional calculations the mass within the galaxy can only explain approx. 1/6 of the necessary centripetal acceleration. - If we assume that the gravitational field is caused not by the mass of the stars but, for example, by the number of elementary particles of which the stars are made up, then we are close to finding a solution which does not call for assuming things like " dark matter" or undetected elementary particles.For details look here


  2. Dark Energy: is a phantom because the acceleration of supernovae is only a seeming result of the evaluation. The acceleration in fact disappears if it is accepted that the speed of light was greater in the past. This latter assumption also solves other open problems of cosmology, by the way. For details look here


  3. Quantum Gravity: According to chapter 6, the phenomenon of gravity is a very weak side effect of the strong interaction. On the other hand, as the strong interaction is fully covered by quantum mechanics, any discrepancy between QM and gravity disappears.

7.1  The "Dark Matter" Phenomenon

Some decades ago the rotational speed within and around big galaxies was discovered to conflict with the equilibrium speed determined on the basis of standard gravity. Figure 7.1 shows the discrepancy for the galaxy NGC 3198.
   

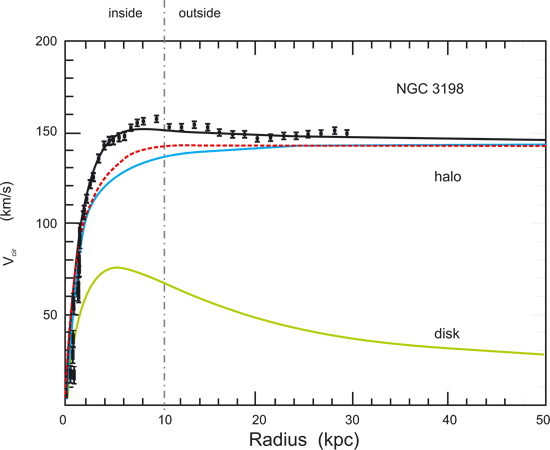Figure 7.1: Equilibrium conflict for the galaxy NGC 3198
(The radius of the galaxy is 10 kpc)

 
Top
 
The solid (green) curve labelled "disk" is the rotational speed as a function of the radius based on a normal gravitational calculation. The uppermost individual values are measurements of the actual speed; a curve (also solid, black) is fitted through these measurements. The intermediate solid (blue) line labelled "halo" describes the distribution of the assumed "dark matter" that is required in order to explain the measured values.

The red dotted line, which is very close to the "halo" curve, follows from the assumption described above, whereby every elementary particle contributes equally to the gravitational field. It represents the contribution of light particles, i.e. neutrinos and photons. In the drawing, the height of this line has been chosen to fit the needs of this diagram, but it fits the assumed data within a tolerance of a factor of 2-3; its curvature, however, is given by the natural distribution of the light particles and is not parameterised.

Of the light particles mentioned, the photons are mainly generated by the hot, bright stars at the centre of the galaxy. The neutrinos are similarly generated by the nuclear processes within the stars, the sources of which are also mostly in or close to the centre of the galaxy. These particles create a continuous flow away from the centre at the speed of light c (or almost this speed). This flow causes their spatial distribution to be

     
  where ρ is the density of the particles and r is the distance from the centre of the galaxy. The number of particles N within a sphere up to a radius r0 is then
     
  The acceleration a towards the centre of the gravitational field (with r0 here renamed r) is
     
  The centrifugal acceleration on the other hand is
     
 

In order to keep these two accelerations in a balance, it follows for the orbital speed v that
     
 

This is the reason for the curvature of the red dotted line in figure 7.1, and so it provides the necessary contribution to the gravitational field which is elsewhere attributed to so-called "dark matter".
 

8  Conclusion

We have shown that gravity is not the force # 4 but a refractive process that acts on all particles. The refraction approach agrees with the results found by Einstein’s method, at least up to the Schwarzschild solution, as has been demonstrated here. And it is easy enough to be taught at a college level.

This approach provides answers to several open questions about gravity:
 
 

1. The weakness of this effect (which is primarily not a force)
2. The attracting-only effect.

The investigation of the cause of the related processes explains

1. The phenomenon called "dark matter"
2. The unresolved conflict with quantum mechanics called "quantum gravity".

The related understanding of relativity in general solves the apparent problem of dark energy in a very easy - and physical - way.

Generally speaking, there is no longer any need for the assumption of 4-dimensional curved space-time in order to explain the phenomena described above. All phenomena of general relativity are caused by the variation of the speed of light c in a gravitational field. - In addition we must accept that the mass of an object is not the cause of the object's gravitational field.

An explanation of the 'Origin of (inertial) Mass' is also available.

Details of the calculations given in the preceding are presented in the appendix (pdf-version), and in a book series [1].
   

4  References

[1] Michael C. Duffy and Joseph Levy, Ether Space-Time & Cosmology, Vol. 3, Apeiron (2009) 143 – 192


NOTE:

The concept of mass-independent gravitation was first presented at the Spring Conference of the German Physical Society (Deutsche Physikalische Gesellschaft) on 5 March 2005 in Berlin by Albrecht Giese.

 
Comments are welcome.

Subtitles: The Origin of Gravitation . Massfree Gravity .
2024-07-04
Top