








 |
||||||||||||||||
|
|
|
 |
|
|
|
|
|
 |
|
|
|
 |
|
|
|
|
 |
 |
 |
 |
|
 |
|
|
|||||||||
|
Why is Time Slowed Down in Motion? The time delay of every kinematic process is the consequence of the fact that matter is built by particles that oscillate permanently at the speed of light. There are good reasons to assume that elementary particles are built by two constituents. These constituents have no mass and orbit each other at the speed of light. If such an elementary particle is set into motion, but its constituents still have to maintain the speed of light in relation to a fixed reference frame, then the orbital frequency is reduced in the way predicted by the theory of relativity. This behaviour propagates to every higher structure at motion. This means also that every clock will go slower at motion.
According to the Basic Model of Matter an elementary particle comprises two basic particles which are bound to each other so as to maintain a specific distance. These two basic particles orbit each other at the speed of light. Consider now the situation where this configuration, which means the elementary particle, is set to motion, but its constituents, the basic particles, are still restricted to maintain exactly the speed of light with respect to a reference frame at rest. The basic particles will now follow a complex path in relation to this frame at rest. The result is that the period of their circular motion will be extended and their orbital frequency reduced. The according calculation is presented in the following chapters.
First the easiest case: If two basic particles are orbiting each other and this circling configuration is as a whole set to motion along the axis at some speed v, then both Basic Particles will follow a helical path.
Figure 2.1 |
|||||||||||||||
| The speed of the particle in relation to the reference frame at rest has always to be c. This speed is now the vector sum of the orbital speed q and the speed of the whole configuration v. So, by the well known relation of Pythagoras, there is | ||||||||||||||||
|
|
(2.1) |
|||||||||||||||
| The orbital period T, which is | ||||||||||||||||
|
|
(2.2) |
|||||||||||||||
| where R is the radius of the orbit, changes to T': | ||||||||||||||||
|
|
(2.3) |
|||||||||||||||
| As a consequence, the period is, if compared with the original period, extended by the Lorentz factor: | ||||||||||||||||
|
|
(2.4) |
|||||||||||||||
|
Now the more difficult - general – case: We will evaluate this case in two stages.
- The first stage is a linear motion of an arbitrary direction 3.1 A Linear Motion of an Arbitrary Direction At first we treat the situation at rest. The observer sends a light pulse, which moves from an origin O to a mirror and is reflected back to the origin. The coordinates of the mirror are described by xo and yo as shown in figure 3.1. |
||||||||||||||||
|
|
||||||||||||||||
| The time T+ needed for the light signal for one way is | ||||||||||||||||
|
|
|
|||||||||||||||
| The time T- needed for the way back is the same, so the full time for both ways is: | ||||||||||||||||
|
|
(3.1) |
|||||||||||||||
| Now the corresponding calculation if the observer moves at a speed v into the direction of γ: | ||||||||||||||||
|
|
||||||||||||||||
| The time T’+ needed for the light signal for one way is now | ||||||||||||||||
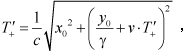 . . |
(3.2) |
|||||||||||||||
| where the way of the light signal is extended by v•T’+ according to the motion of the observer’s system, and the measuring set up is contracted in the y direction by the Lorentz factor | ||||||||||||||||
|
|
|
|||||||||||||||
| Now (3.2) squared | ||||||||||||||||
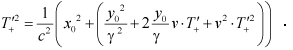 . . |
|
|||||||||||||||
| Reordered | ||||||||||||||||
|
|
|
|||||||||||||||
| now multiplied by γ2 | ||||||||||||||||
|
|
|
|||||||||||||||
| The equation resolved by the standard method: | ||||||||||||||||
|
|
|
|||||||||||||||
|
Here only ‘+’ is applicable as the time is positive. Correspondingly for the way back | ||||||||||||||||
|
|
|
|||||||||||||||
| Now the sum of both ways | ||||||||||||||||
|
|
(3.3) |
|||||||||||||||
| Now inserted | ||||||||||||||||
|
|
|
|||||||||||||||
| yields | ||||||||||||||||
|
|
|
|||||||||||||||
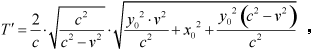 |
|
|||||||||||||||
|
|
|
|||||||||||||||
| Now the dilation is | ||||||||||||||||
|
|
(3.4) |
|||||||||||||||
|
The result here is that every motion forth and back in any direction, which is limited to ‘c’ with respect to the reference frame at rest, is delayed by the Lorentz-Factor γ. Please note that the coordinates xo and yo do not appear in the result, so the result is valid for every direction.
The dilation at a circular motion can now be easily calculated based on the preceding section.
| ||||||||||||||||
|
|
||||||||||||||||
|
This circular motion may have an arbitrary orientation in space. The motion path can be decomposed into pairs of infinitesimal pieces ds of opposite direction, where each pair is, if summed, delayed by the factor of γ as given in section 3.1, eq. (3.4). |
||||||||||||||||
|
Every internal motion in an object at speed 'c' is reduced by the Lorentz factor γ when the whole object is in motion. This conforms to the time dilation in special relativity, but is deduced without any use of the 4-dimensional space-time. |
||||||||||||||||
|
NOTE: The
concept of the
Basic Model of matter
was initially presented at the Spring Conference of the German Physical
Society (Deutsche Physikalische Gesellschaft) on 24 March 2000 in
Dresden by Albrecht Giese. Comments are welcome. (Note: This page is also available as a pdf-file.) 2021-05-15 |
||||||||||||||||