The Acceleration of a System of 2 Particles as a Step-by-Step Process
In the following, we will show in detail how the process of field transfer works, in order to give a better idea of why two particles located at a distance from each other display inertial behaviour. We start with the initial situation in which each particle is at rest, with no resultant force in the potential field of the other particle. Particle B (figure 1) experiences no resultant force at the minimum of the potential due to A, which is symbolised by the relaxed spring on its right-hand side.
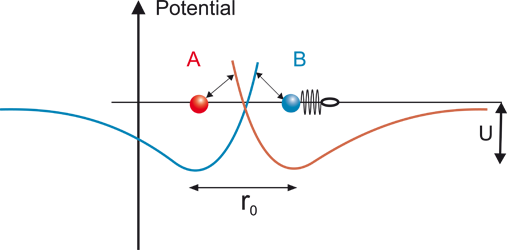
Figure 1
Particles A and B in a force-free equilibrium state
In the next step, particle B is displaced to the right by a certain amount (figure 2). This means that B is moved away from the potential minimum, so a force is required, which is depicted here by the stretching of the spring. (Remark: A sudden change in the position of B is assumed here, which is not physically accurate but helps to understand the process more easily.)
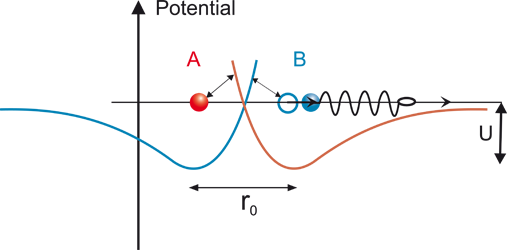
Figure 2
Particle B pulled away from the potential minimum by a force
As a result of displacing B, the field due to B follows B to the right. This happens at the speed of light c. The change in the field requires a time interval Δt
(1)
to propagate from one particle to the other one.
So after a time ½ Δt, the change in the field has moved halfway to A (figure 3).
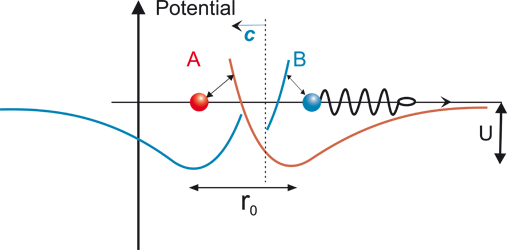
Figure 3
Displacement of field due to B has travelled half the way to A
Then, after a time 1 Δt, the change in the field reaches particle A (figure 4). At this point, particle A instantaneously moves to the right, to the new position of minimum potential.
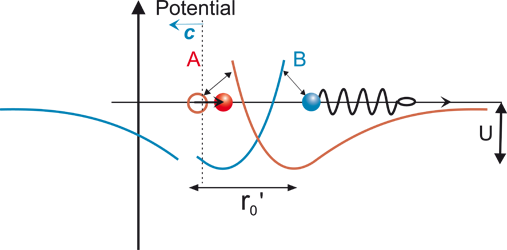
Figure 4
Displacement of field due to B reaches A
A further consequence of this is that the field due to A also moves to the right. So, after a further time interval of ½ Δt, i.e. after 1 ½ Δt overall, it is has covered half the distance to B (figure 5).
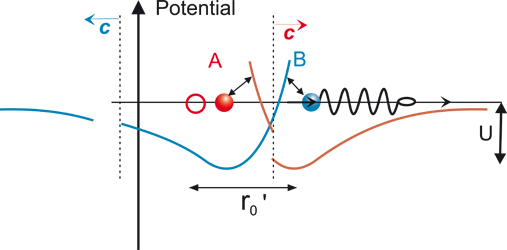
Figure 5
Displacement of field due to A has covered half the distance to B
Finally, after a time 2 Δt, the repositioned field due to A reaches B, so that B is now once again at the minimum potential of the field due to A. This means no force is necessary any more to keep B in its new position as now represented by the relaxed spring (figure 6).
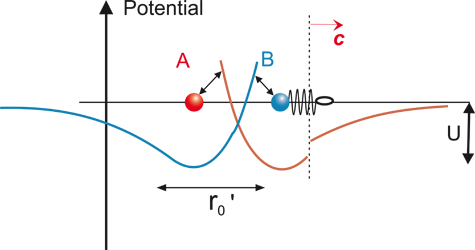
Figure 6
Displacement of field due to A reaches B
The full cycle of the changes of positions and fields shows, that an intermediate force is necessary in order to move this system of 2 particles to a new position.
In fact, the system is not only moved to a new position, but it is now in a state of motion. This
is a consequence of the relativistic contraction of fields in motion. When the fields due to B and A move as a result of displacing the two particles, these
fields contract. Hence at the end of the cycle both particles are located at a reduced distance r’ from each other. The new separation r’ is stable only if the
configuration is moving and vice versa.
This phenomenon, whereby a force must be applied for an intermediate time in order to cause a change of the state of motion, is the physical phenomenon of inertial mass.